In this Python data analysis tutorial, we will focus on how to carry out between-subjects ANOVA in Python. As mentioned in an earlier post (Repeated measures ANOVA with Python) ANOVAs are commonly used in Psychology. We start with a brief introduction to the theory of ANOVA.
If you are more interested in the four methods for one-way ANOVA with Python click here.
In this post, we will learn how to carry out ANOVA using SciPy, calculating it “by hand” in Python, using Statsmodels, and Pyvttbl.
Update: the Python package Pyvttbl is not maintained for a couple of years but there’s a new package called Pingouin. As a bonus, how to use this package is added at the end of the post.
Table of Contents
- Prerequisites
- Introduction to ANOVA
- 6 Steps to Carry Out ANOVA in Python
- ANOVA using Python
- Conclusion: Python ANOVA
- Resources
Prerequisites
In this post, you will need to install the following Python packages:
- SciPy
- NumPy
- Pandas
- Statsmodels
- Pingouin
Of course, you don’t have to install all of these packages to perform the ANOVA with Python. Now, if you only want to do the data analysis you can choose to install either SciPy, Statsmodels, or Pingouin. However, Pandas will be used to read the example datasets and carry out some simple descriptive stats and data visualization. Installing Python packages can be done with either pip or conda, for example. Here’s how to install all of the above packages:
pip install scipy numpy pandas statsmodels pingouinCode language: Bash (bash)Now, pip can also be used to install a specific version of a package. To install an older version you add “==” followed by the version you want to be installed. In the next section, you will get a brief introduction to ANOVA, in general. Of course, if you only plan to use one of the packages, you can install one. Note, however, if you install statsmodels with e.g. pip you will install also SciPy, NumPY, and Pandas.
Introduction to ANOVA
Before we learn how to do ANOVA in Python, we briefly discuss what ANOVA is. ANOVA is a means of comparing the ratio of systematic variance to unsystematic variance in an experimental study. Variance in the ANOVA is partitioned into total variance, variance due to groups, and variance due to individual differences.
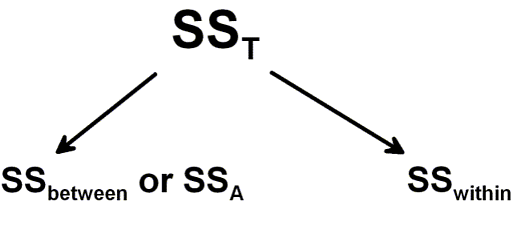
The ratio obtained when making this comparison is known as the F-ratio. A one-way ANOVA can be seen as a regression model with a single categorical predictor. This predictor usually has two plus categories. A one-way ANOVA has a single factor with J levels. Each level corresponds to the groups in the independent measures design.
The general form of the model, which is a regression model for a categorical factor with J levels, is:
$latex y_i = b_0+b_1X_{1,i} +…+b_{j-1,i} + e_i&s=2$
There is a more elegant way to parametrize the model. This way, the group means are represented as deviations from the grand mean by grouping their coefficients under a single term. I will not go into detail on this equation:
$latex y_{ij} = \mu_{grand} + \tau_j + \varepsilon_{ij}&s=2$
As for all parametric tests the data need to be normally distributed (each group’s data should be roughly normally distributed) for the F-statistic to be reliable. Each experimental condition should have roughly the same variance (i.e., homogeneity of variance), the observations (e.g., each group) should be independent, and the dependent variable should be measured on at least an interval scale.
Assumptions
As with all parametric tests, also ANOVA has several assumptions. First of all, the groups have to be independent of each other. Second, the residuals must be normally distributed (within each group). Third, there have to be equal variances between all groups. The homogeneity of variances can be tested with Bartlett’s and Levene’s tests in Python (e.g., using SciPy), and the normality assumption can be tested using the Shapiro-Wilks test or by examining the distribution. Note, if your data is skewed, you can transform it using, e.g., the log transformation in Python.
A Priori Tests
When conducting ANOVA in Python, it is usually best to restrict the testing to a small set of possible hypotheses. Furthermore, these tests should be motivated by theory and are known as a priori or planned comparisons. As the names imply, these tests should be planned before collecting data.
Post-Hoc Tests (Pairwise Comparisons) in Python
Even though studies can have a strong theoretical motivation and a priori hypotheses, there will be times when the pattern occurs after the data is collected. Note, if there are many possible tests, these post-hoc tests, the error rate is determined by the number of tests that might have been carried out.
There are several possible post-hoc tests that can be carried out. In this ANOVA in Python tutorial, we will use Tukey’s honestly significant difference (Tukey-HSD) test
6 Steps to Carry Out ANOVA in Python
Now, before getting into details, here are six steps to carry out ANOVA in Python:
- Install the Python package Statsmodels (
pip install statsmodels) - Import statsmodels api and ols:
import statsmodels.api as smandfrom statsmodels.formula.api import ols - Import data using Pandas
- Set up your model
mod = ols('weight ~ group', data=data).fit() - Carry out the ANOVA:
aov_table = sm.stats.anova_lm(mod, typ=2) - Print the results:
print(aov_table)
Now, sometimes when we install packages with Pip we may notice that we don’t have the latest version installed. If we want to, we can of course, update pip to the latest version using pip or conda.
ANOVA using Python
In the four Python ANOVA examples in this tutorial we are going to use the dataset “PlantGrowth” that originally was available in R. However, it can be downloaded using this link: PlantGrowth. In the first three examples, we are going to use Pandas DataFrame. All three Python ANOVA examples below are using Pandas to load data from a CSV file. Note, we can also use Pandas read excel if we have our data in an Excel file (e.g., .xlsx).
import pandas as pd
datafile = "PlantGrowth.csv"
data = pd.read_csv(datafile)
#Create a boxplot
data.boxplot('weight', by='group', figsize=(12, 8))
ctrl = data['weight'][data.group == 'ctrl']
grps = pd.unique(data.group.values)
d_data = {grp:data['weight'][data.group == grp] for grp in grps}
k = len(pd.unique(data.group)) # number of conditions
N = len(data.values) # conditions times participants
n = data.groupby('group').size()[0] #Participants in each conditionCode language: Python (python)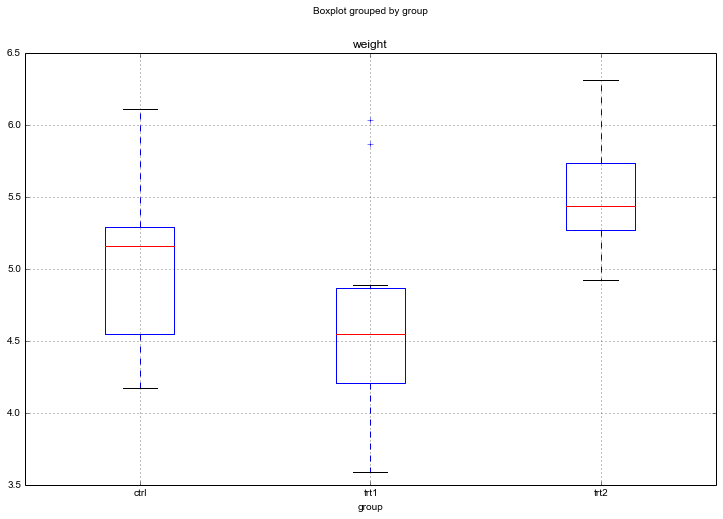
Judging by the Boxplot, there are differences in the dried weight for the two treatments. However, easy to visually determine whether the treatments differ from the control group.
Python ANOVA YouTube Video:
- If you want to learn how to work with Pandas dataframe see the post A Basic Pandas Dataframe Tutorial
- Also, see the Python Pandas Groupby Tutorial for more about working with the groupby method.
- How to Perform a Two-Sample T-test with Python: 3 Different Methods or carry out the Mann-Whitney U test in Python.
ANOVA in Python using SciPy
We start this Python ANOVA tutorial using SciPy and its method f_oneway from stats.
from scipy import stats
F, p = stats.f_oneway(d_data['ctrl'], d_data['trt1'], d_data['trt2'])Code language: Python (python)One problem with using SciPy is that following APA guidelines, we should also effect size (e.g., eta squared) and Degree of freedom (DF). DFs needed for the example data are easily obtained.
DFbetween = k - 1
DFwithin = N - k
DFtotal = N - 1Code language: Python (python)However, if we want to calculate eta-squared we need to do more computations. Thus, the next section will deal with calculating a one-way ANOVA using the Pandas DataFrame and Python code.
Calculating using Python (i.e., pure Python ANOVA)
A one-way ANOVA in Python is quite easy to calculate so below I am going to show how to do it. First, we need to calculate the Sum of Squares Between (SSbetween), Sum of Squares within (SSwithin), and Sum of Squares Total (SSTotal).
The sum of Squares Between
We start by calculating the Sum of Squares between. Sum of Squares Between is the variability due to interaction between the groups. The sum of Squares Between is sometimes known as the Sum of Squares of the Model.
$latex SSbetween = \frac{\sum(\sum k_i) ^2} {n} – \frac{T^2}{N}&s=2$SSbetween = (sum(data.groupby('group').sum()['weight']**2)/n) \
- (data['weight'].sum()**2)/NCode language: Python (python)How to Calculate the Sum of Squares Within
The variability in the data due to differences within people. The calculation of Sum of Squares Within can be carried out according to this formula:
$latex SSwithin = \sum Y^2 – \frac{\sum (\sum a_i)^2}{n}&s=2$sum_y_squared = sum([value**2 for value in data['weight'].values])
SSwithin = sum_y_squared - sum(data.groupby('group').sum()['weight']**2)/nCode language: Python (python)Calculation of Sum of Squares Total
The sum of Squares Total will be needed to calculate eta-squared later. This is the total variability in the data.
$latex SStotal = \sum Y^2 – \frac{T^2}{N}&s=2$SStotal = sum_y_squared - (data['weight'].sum()**2)/NCode language: Python (python)How to Calculate Mean Square Between
The mean square between is the sum of squares within divided by degree of freedom between.
MSbetween = SSbetween/DFbetweenCalculation of Mean Square Within
The mean Square within is also an easy calculation;
MSwithin = SSwithin/DFwithinCode language: Python (python)Calculating the F-value
Here is how we calculate the F-value in Python:
F = MSbetween/MSwithinCode language: Python (python)To reject the null hypothesis, we check if the obtained F-value is above the critical value for rejecting the null hypothesis. We could look it up in an F-value table based on the DFwithin and DFbetween. However, there is a method in SciPy for obtaining a p-value.
p = stats.f.sf(F, DFbetween, DFwithin)Code language: Python (python)Finally, we are also going to calculate the effect size. We start with the commonly used eta-squared (η² ):
eta_sqrd = SSbetween/SStotalCode language: Python (python)However, eta-squared is somewhat biased because it is based purely on sums of squares from the sample. No adjustment is made for the fact that what we are aiming to do is to estimate the effect size in the population. Thus, we can use the less biased effect size measure Omega squared:
om_sqrd = (SSbetween - (DFbetween * MSwithin))/(SStotal + MSwithin)Code language: Python (python)The results from both the SciPy and the above method can be reported according to APA style; F(2, 27) = 4.846, p = .016, η² = .264. If you want to report Omega Squared: ω2 = .204. That was it, now we know how to do ANOVA in Python by calculating everything “by hand”.
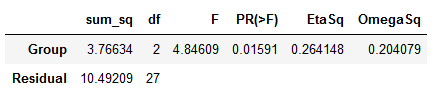
ANOVA in Python using Statsmodels
In this section of the Python ANOVA tutorial, we will use Statsmodels. First, we use the ordinary least squares (ols) method and then the anova_lm method. Also, if you are familiar with R-syntax, Statsmodels have a formula API where our model is very intuitively formulated.
Here are three simple steps for carrying out ANOVA using Statsmodels:
Time needed: 1 minute
The ANOVA how-to below assumes that the data is in a Pandas dataframe (i.e., df).
- Import the needed Python packages
First, we import statsmodels API and ols:
- Set up the ANOVA model
Second, we use ols to set up our model using a formula
- Carry out the ANOVA
We can now use anova_lm to carry out the ANOVA in Python
In the ANOVA example below, we import the API and the formula API. Second, we use ordinary least squares regression with our data. The object obtained is a fitted model we later use with the anova_lm method to obtain an ANOVA table.
In the final part of this section, we will carry out pairwise comparisons using Statsmodels.
import statsmodels.api as sm
from statsmodels.formula.api import ols
mod = ols('weight ~ group',
data=data).fit()
aov_table = sm.stats.anova_lm(mod, typ=2)
print(aov_table)Code language: Python (python)ANOVA Python table:
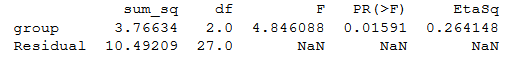
Note, no effect sizes are calculated when we use Statsmodels. To calculate eta squared, we can use the sum of squares from the table:
esq_sm = aov_table['sum_sq'][0]/(aov_table['sum_sq'][0]+aov_table['sum_sq'][1])aov_table['EtaSq'] = [esq_sm, 'NaN']print(aov_table)Code language: Python (python)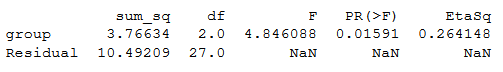
Python ANOVA: Pairwise Comparisons
It is, of course, also possible to calculate pairwise comparisons for our Python ANOVA using Statsmodels. In the next example, we are going to use the t_test_pairwise method. Conducting post-hoc tests, corrections for familywise error can be carried out using several methods (e.g., Bonferroni, Šidák)
pair_t = mod.t_test_pairwise('group')
pair_t.result_frameCode language: Python (python)
Note, if we want to use another correction method, we add the parameter method and add “bonferroni” or “sidak”, for instance (e.g., method=”sidak”).
If we were to carry out regression analysis, using Python, we might have to convert the categorical variables to dummy variables using Pandas get_dummies() method.
Python ANOVA using pyvttbl anova1way
In this section, we will learn how to carry out an ANOVA in Python using the method anova1way from the Python package pyvttbl. This package also has a DataFrame method. We have to use this method instead of Pandas DataFrame to be able to carry out the one-way ANOVA in Python. Note, Pyvttbl is old and outdated. It requires Numpy to be at most version 1.1.x or else you will run into an error ( “unsupported operand type(s) for +: ‘float’ and ‘NoneType’”).
This can, of course, be solved by downgrading Numpy (see my solution using a virtual environment Step-by-step guide for solving the Pyvttbl Float and NoneType error). However, it may be better to use pingouin for carrying out Python ANOVAs (see the next section of this blog post).
from pyvttbl import DataFrame
df=DataFrame()
df.read_tbl(datafile)
aov_pyvttbl = df.anova1way('weight', 'group')
print aov_pyvttblCode language: Python (python)Output anova1way
Anova: Single Factor on weight
SUMMARY
Groups Count Sum Average Variance
============================================
ctrl 10 50.320 5.032 0.340
trt1 10 46.610 4.661 0.630
trt2 10 55.260 5.526 0.196
O'BRIEN TEST FOR HOMOGENEITY OF VARIANCE
Source of Variation SS df MS F P-value eta^2 Obs. power
===============================================================================
Treatments 0.977 2 0.489 1.593 0.222 0.106 0.306
Error 8.281 27 0.307
===============================================================================
Total 9.259 29
ANOVA
Source of Variation SS df MS F P-value eta^2 Obs. power
================================================================================
Treatments 3.766 2 1.883 4.846 0.016 0.264 0.661
Error 10.492 27 0.389
================================================================================
Total 14.258 29
POSTHOC MULTIPLE COMPARISONS
Tukey HSD: Table of q-statistics
ctrl trt1 trt2
=================================
ctrl 0 1.882 ns 2.506 ns
trt1 0 4.388 *
trt2 0
=================================
+ p < .10 (q-critical[3, 27] = 3.0301664694)
* p < .05 (q-critical[3, 27] = 3.50576984879)
** p < .01 (q-critical[3, 27] = 4.49413305084)Code language: HTTP (http)We get a lot of more information using the anova1way method. What may be of particular interest here is that we get results from a post-hoc test (i.e., Tukey HSD). Whereas the ANOVA only lets us know that there was a significant effect of treatment the post-hoc analysis reveals where this effect may be (between which groups).
If you have more than one dependent variable a multivariate method may be more suitable. Learn more on how to carry out a Multivariate Analysis of Variance (ANOVA) using Python:
Python ANOVA using Pingouin (bonus)
In this section, we will learn how to carry out ANOVA in Python using the package pingouin. This package is, as with Statsmodels, very simple to use. If we want to carry out an ANOVA, we use anova.
import pandas as pd
import pingouin as pg
data = "https://vincentarelbundock.github.io/Rdatasets/csv/datasets/PlantGrowth.csv"
df = pd.read_csv(data, index_col=0)
aov = pg.anova(data=df, dv='weight', between='group', detailed=True)
print(aov)Code language: Python (python)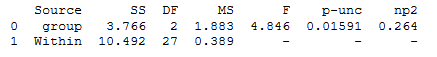
As seen in the ANOVA table above, we get the degrees of freedom, the mean square error, F- and p-values, and the partial eta squared when using pingouin.
Pairwise Comparisons in Python (Tukey-HSD)
One neat thing with Pingouin is that we can also carry post-hoc tests. We are now going to carry out the Tukey-HSD test as a follow-up on our ANOVA. This is also very simple; we use the pairwise_tukey method to carry out the pairwise comparisons:
pt = pg.pairwise_tukey(dv='weight', between='group', data=df)
print(pt)Code language: Python (python)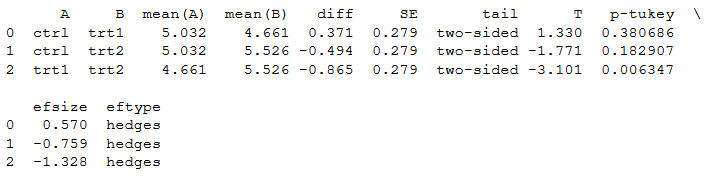
Note, if we want another type of effect size we can add the argument effsize and choose between six different effect sizes (or none): cohen, hedges, glass, eta-square, odds-ratio, and AUC. In the last code example we change the default effect size (hedges) to Cohen:
cpt = pg.pairwise_tukey(dv='weight', between='group', effsize='cohen', data=df)
print(pt)Code language: Python (python)Conclusion: Python ANOVA
That is it! In this tutorial, you learned four methods that let you carry out one-way ANOVAs using Python. There are other ways to deal with the tests between the groups (e.g., the post-hoc analysis).
One could carry out Multiple Comparisons (e.g., t-tests between each group. Remember to correct for familywise error!) or Planned Contrasts. In conclusion, doing ANOVAs in Python is pretty simple.
Resources
Here are some more Python tutorials:
- Python Scientific Notation & How to Suppress it in Pandas & NumPy
- How to Plot a Histogram with Pandas in 3 Simple Steps
- Find the Highest Value in Dictionary in Python
Heck of a job there, it aboesutlly helps me out.
Thank you for your effort, very clearly set.
However, I am hitting a problem using ANOVA1Way, I wonder if you have any suggestions. When I make a copy of PlantGrowth.csv and type in new numbers for “weight” and then run your code, I get:
Error: new-line character seen in unquoted field – do you need to open the file in universal-newline mode?
Thanks and Regards
Hey Umit,
I cannot really answer your question since the error does not happen on my computer. I did find this: http://stackoverflow.com/questions/17315635/csv-new-line-character-seen-in-unquoted-field-error. Maybe you could test that and see if it works. If you solve your problem, or have already solved it, please let me know how.
Thanks and regards,
Erik
Hi Erik,
thanks for the great post. I wanted to offer an update to part 2 (python based ANOVA) for when the groups have different sample sizes.
First, rewrite the calculation for n:
n = data.groupby(var).size().values
Then the calculation for SSbetween and SSwithin needs to be modified:
SSbetween = (sum(data.groupby(var).sum()[‘LogSalePrice’].values**2/n)) – (data[‘LogSalePrice’].sum()**2)/N
SSwithin = sum_y_squared – sum(data.groupby(var).sum()[‘LogSalePrice’].values**2/n)
It just takes the division by n (element-wise) inside the outer sum in both cases.
I tested this by comparing with the output from f_oneway and it seems to work. It should also generalize well to the case where n is the same for all groups.
Thanks again for the write-up!
Hi Joel,
thanks for your comment and thanks for the update! I’ll add this to the post (with a reference to your comment, of course).
Erik
Thanks for your post… It was super useful for me
Hi Erik!
Thank you for the post. I’ve been working recently on a Python stats package that implements several ANOVA-related functions and post-hocs tests. Just thought I’d mention it in case this would turn useful to you or others: https://pingouin-stats.org/
All the best,
Raphael
Hey Raphael,
This looks really interesting! Will install this later today and play around with it. I might just add it to one of my posts listing useful Python packages. We’ll see!
Maybe I’ll also update this post (or write a new one). I’ll send you an email, if I do.
Thanks for letting us know about the package,
Best,
Erik