Descriptive Statistics in Python using Pandas

in this Python and Pandas tutorial, you will learn how to calculate descriptive statistics in Python using Pandas. First, you will get a brief description of what descriptive statistics is. After that, you will get a quick answer to a the question “how can I calculate descriptive statistics in Python”. In the next subsections, we will simulate data so that we have some data to calculate summary statistics on.

In the next sections, we will go through how to get a table with summary statistics of the variables in the Pandas dataframe, calculate central tendency (e.g., mean, median), and then a section how to calculate measures of variability (e.g., standard deviation, variance).Finally, you will learn how to save the descriptive statistics you have calcualted to a .csv file.

Table of Contents

• Descriptive Statistics
  • Simulate Data using Python and NumPy
  • Import Data in Python
  • Descriptive statistics using Pandas in Python
    • Central tendency in Python
    • Pandas Mean
    • Geometric & Harmonic Mean in Python
      • Geometric Mean using Scipy & Pandas
      • Harmonic using Scipy & Pandas
    • Trimmed Mean in Python
    • Pandas Median
    • Scipy Mode
  • Measures of Variability in Python
    • Pandas Standard deviation
    • Interquartile Range in Pandas
    • Pandas Variance
• Saving Summary Statistics to a CSV
• Conclusion

Descriptive Statistics

After data collection, most Psychology researchers use different ways to summarise the data. In this tutorial, we will learn how to do descriptive statistics in Python. Python, being a programming language, enables us many ways to carry out descriptive statistics.

• A Basic Pandas Dataframe Tutorial for Beginners

Actually, Pandas offers an API similar to Rs. I think that the dataframe in R is very intuitive to use and Pandas offers a DataFrame method similar to Rs. Also, many Psychology researchers may have experience of R

Thus, in this tutorial, we will learn how to do descriptive statistics using Pandas, but we will also use the Python packages NumPy, and SciPy. First, we start by using Pandas for obtaining summary statistics and some variance measures. After that, we continue with the central tendency measures (e.g., mean and median) using Pandas and NumPy.

Furthermore, the harmonic, the geometric, and the trimmed mean cannot be calculated using Pandas or NumPy. For these measures of central tendency, we will use SciPy. Towards the end, we learn how to get some measures of variability (e.g., variance using Pandas).

import numpy as np
from pandas import DataFrame as df
from scipy.stats import trim_mean, kurtosis
from scipy.stats.mstats import mode, gmean, hmeanCode language: Python (python)

Simulate Data using Python and NumPy

In this section, of the Python summary statistics tutorial, we are going to simulate data to work with. Many times in experimental psychology response time is the dependent variable. In this descriptive statistics in Python example, we will first simulate an experiment in which the dependent variable is response time to some arbitrary targets.

Furthermore, the simulated data will have two independent variables (IV, “iv1” have 2 levels and “iv2” have 3 levels). Here, the data are simulated at the same time as a Pandas dataframe is created and the first descriptive statistics are obtained using Pandas describe.

N = 20
P = ["noise","quiet"]
Q = [1,2,3]

values = [[998,511], [1119,620], [1300,790]]

mus = np.concatenate([np.repeat(value, N) for value in values])

data = df(data = {'id': [subid for subid in range(N)]*(len(P)*len(Q))
    ,'iv1': np.concatenate([np.array([p]*N) for p in P]*len(Q))
    ,'iv2': np.concatenate([np.array([q]*(N*len(P))) for q in Q])
    ,'rt': np.random.normal(mus, scale=112.0, size=N*len(P)*len(Q))})Code language: Python (python)

Import Data in Python

In the example above we simulated data. We can, of course, use our own stored data. If you need how to work with Excel files see this Pandas read and write Excel files tutorial. Furthermore, it is also possible to load data into a Pandas dataframe is to read CSV files with the read_csv() method.

Finally, we can import data from SPSS files, SAS (.dta) files, and Stata (.7bdat) files using Pandas. Now, it is also possible to read other types of files with just Python so make sure to check out the post about how to read a file in Python. Notice, to calculate summary statistics for specific columns we need to know the variable names in the dataset. One way to to this, is to get the column names using the columns method.

Descriptive statistics using Pandas in Python

In this section, we will use Pandas describe method to carry out summary statistics in Python.

data.describe()Code language: Python (python)

Pandas will output summary statistics by using this method. Output is a table, as you can see below.

• Save

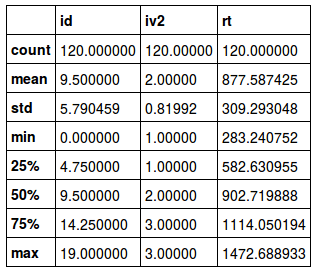
Typically, a researcher is interested in the descriptive statistics of the IVs. Therefore, we group the data by these (i.e., iv1, iv2). Again, using the describe method on the grouped we get summary statistics for each level in each IV.

As can be seen from the output it is somewhat hard to read. Note, the method unstack is used to get the mean, standard deviation (std), etc as columns and it becomes somewhat easier to read.

grouped_data = data.groupby(['iv1', 'iv2'])
grouped_data['rt'].describe().unstack()Code language: Python (python)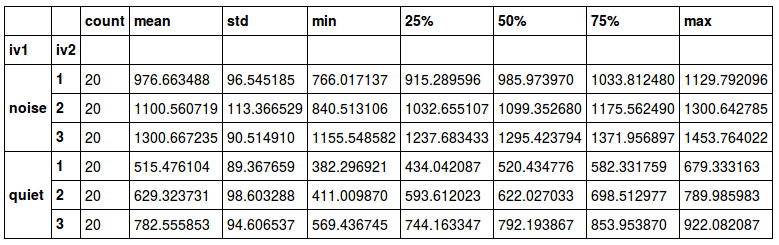

• Save

For more on how to use Pandas groupby method see the Python Pandas Groupby Tutorial. If you, on the other hand, don’t have any grouping variable you can use the describe method on your dataframe (e.g., data in this example). If you only need to get the unique values of e.g. a factor you can use Pandas value_counts() to count occurrences in a column.

Central tendency in Python

In this Python descriptive statistics tutorial, we will focus on the measures of central tendency. Often, we want to know something about the “average” or “middle” of our data. Using Pandas and NumPy the two most commonly used measures of central tendency can be obtained; the mean and the median. Moreover, the mode and the trimmed mean can also be obtained using Pandas but I will use methods from  SciPy.

Pandas Mean

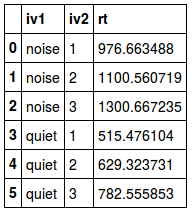
If we are only interested in one summary statistic, we can calculate them separately. When we use Pandas, there are at least two ways of doing this using our grouped data. First, Pandas have the method mean;

grouped_data['rt'].mean().reset_index()Code language: Python (python)

But the method aggregate in combination with NumPys mean can also be used;

grouped_data['rt'].aggregate(np.mean).reset_index()Code language: Python (python)

Both methods will give the same output but the aggregate method have some advantages that I will explain later.

• Save

Here’s a YouTube Video on how to use Pandas describe() to do descriptive stats:

Geometric & Harmonic Mean in Python

Sometimes when are calculating summary statistics, the geometric or harmonic mean can be of interest. In Python, these two descriptive statistics can be obtained using the method apply with the methods gmean and hmean (from SciPy) as arguments. That is, there is no method in Pandas or NumPy that enables us to calculate geometric and harmonic means.

Geometric Mean using Scipy & Pandas

In Pandas, we can use the apply method to input another function, such as gmean from SciPy. In the next Pandas descriptive statistics examples, we are going to use apply.

grouped_data['rt'].apply(gmean, axis=None).reset_index()Code language: Python (python)

Harmonic using Scipy & Pandas

In this, Python Pandas summary statistics example, we use apply together with hmean to obtain the harmonic mean:

grouped_data['rt'].apply(hmean, axis=None).reset_index()Code language: Python (python)

Trimmed Mean in Python

Trimmed means are, at times, used. Pandas or NumPy seems not to have methods for obtaining the trimmed mean. However, we can use the method trim_mean from SciPy . By using apply to our grouped data we can use the function (‘trim_mean’) with an argument that will make 10 % av the largest and smallest values to be removed.

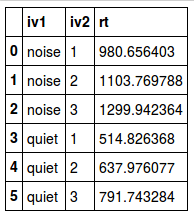
trimmed_mean = grouped_data['rt'].apply(trim_mean, .1)
trimmed_mean.reset_index()Code language: JavaScript (javascript)

Output from the mean values above (trimmed, harmonic, and geometric means):

Save

Save

Save

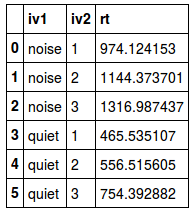
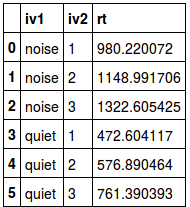
Pandas Median

In Python, using Pandas, there are two methods to calculate the median. In the example below we use Pandas median  and aggregate together with NumPy’s median.

grouped_data['rt'].median().reset_index()
grouped_data['rt'].aggregate(np.median).reset_index()Code language: Python (python)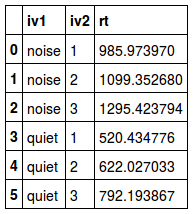

• Save

Scipy Mode

In this section, of the descriptive statistics in Python tutorial, we will use ScipPy to get the mode. Now, there is a method (i.e., pandas.DataFrame.mode()) for getting the mode for a DataFrame object. However, in this example, we will use mode from SciPy because Pandas mode cannot be used on grouped data.

grouped_data['rt'].apply(mode, axis=None).reset_index()Code language: Python (python)

Most of the time we probably would want to see all measures of central tendency at the same time. Luckily, the method aggregate enables us to use many NumPy and SciPy methods. In the example below, the standard deviation (std), mean, harmonic mean,  geometric mean, and trimmed mean are all in the same output. Note that we will have to add the trimmed means afterward.

descr = grouped_data['rt'].aggregate([np.median, np.std, np.mean]).reset_index()
descr['trimmed_mean'] = pd.Series(trimmed_mean.values, index=descr.index)
descrCode language: Python (python)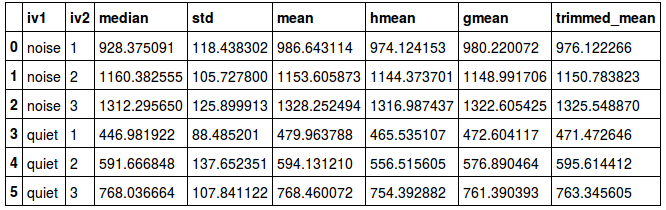

• Save

Measures of Variability in Python

In this section, of the summary statistics in Python post, we will continue and learn how to calculate measures of variability in Python. Now, central tendency (e.g., the mean & median) is not the only type of summary statistic that we want to calculate. We will probably also want to have a look at a measure of the variability of the data.

Pandas Standard deviation

Here’s how to calculate the standard deviation in Python with Pandas:

grouped_data['rt'].std().reset_index()Code language: Python (python)

Interquartile Range in Pandas

In this example, we will use Pandas quantile  to calculate the IQR. Note that here the use unstack()  also get the quantiles as columns and the output is easier to read.

grouped_data['rt'].quantile([.25, .5, .75]).unstack()Code language: Python (python)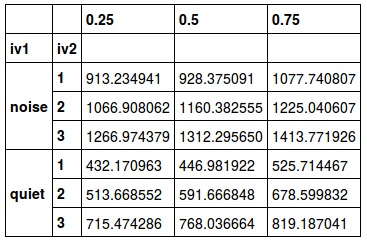

• Save

Pandas Variance

Variance is easy to calculate using Pandas. In the example below, we use the var method to carry out the calculation together with the reset_index method.

grouped_data['rt'].var().reset_index()Code language: Python (python)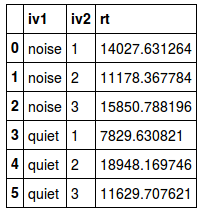

• Save

Saving Summary Statistics to a CSV

If we want to save our descriptive statistics, calculated in Python, we can use the Pandas dataframe to_csv method. In the example below, we are saving the Pandas dataframe descr created earlier to a CSV file:

descr.to_csv('Descriptive_Statistics_in_Python.csv', index=False)Code language: Python (python)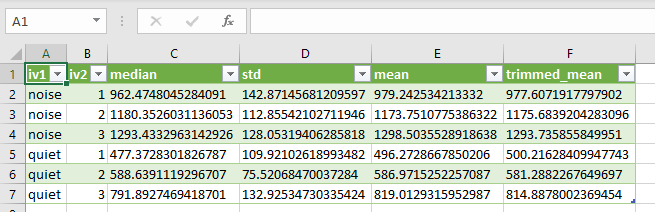

• Save

Finally, if we save a lot of CSV files, using Pandas, with descriptive statistics from different datasets we may, in the future, also learn how to rename a file in Python.

Conclusion

That is all. Now you know how to obtain some of the most common descriptive statistics using Python. Pandas, NumPy, and SciPy really makes these calculation almost as easy as doing it in graphical statistical software such as SPSS. One great advantage of the methods apply and aggregate is that we can input other methods or functions to obtain other types of descriptives.

Here’s a Jupyter Notebook with all the examples above.

Update: Recently, I learned some methods to explore response times visualizing the distribution of different conditions: Exploring response time distributions using Python.

I am sorry that the images (i.e., the tables) are so ugly. If you happen to know a good way to output tables and figures from Python (something like Knitr & Rmarkdown) please let me know.