Previously I have shown how to analyze data collected using within-subjects designs using rpy2 (i.e., R from within Python) and Pyvttbl. In this post I will extend it into a factorial ANOVA using Python (i.e., Pyvttbl). In fact, we are going to carry out a Two-way ANOVA but the same method will enable you to analyze any factorial design. I start with importing the Python libraries that are going to be use.
import numpy as np
import pyvttbl as pt
from collections import namedtupleCode language: Python (python)Numpy is going to be used to simulate data. I create a data set in which we have one factor of two levels (P) and a second factor of 3 levels (Q). As in many of my examples the dependent variable is going to be response time (rt) and we create a list of lists for the different population means we are going to assume (i.e., the variable ‘values’). I was a bit lazy when coming up with the data so I named the independent variables ‘iv1’ and ‘iv2’. However, you could think of iv1 as two different memory tasks; verbal and spatial memory. Iv2 could be different levels of distractions (no distraction, synthetic sounds, and speech, for instance).
Table of Contents
- Simulate data
- Two-way ANOVA for within-subjects design in Python
- Output ANOVA table
- Alternative Data Analysis Techniques
Simulate data
N = 20
P = [1,2]
Q = [1,2,3]
values = [[998,511], [1119,620], [1300,790]]
sub_id = [i+1 for i in xrange(N)]*(len(P)*len(Q))
mus = np.concatenate([np.repeat(value, N) for value in values]).tolist()
rt = np.random.normal(mus, scale=112.0, size=N*len(P)*len(Q)).tolist()
iv1 = np.concatenate([np.array([p]*N) for p in P]*len(Q)).tolist()
iv2 = np.concatenate([np.array([q]*(N*len(P))) for q in Q]).tolist()
Sub = namedtuple('Sub', ['Sub_id', 'rt','iv1', 'iv2'])
df = pt.DataFrame()
for idx in xrange(len(sub_id)):
df.insert(Sub(sub_id[idx],rt[idx], iv1[idx],iv2[idx])._asdict())Code language: Python (python)I start with a boxplot using the method boxplot from Pyvttbl. As far as I can see there is not much room for changing the plot around. We get this plot and it is really not that beautiful.
df.box_plot('rt', factors=['iv1', 'iv2'])Code language: Python (python)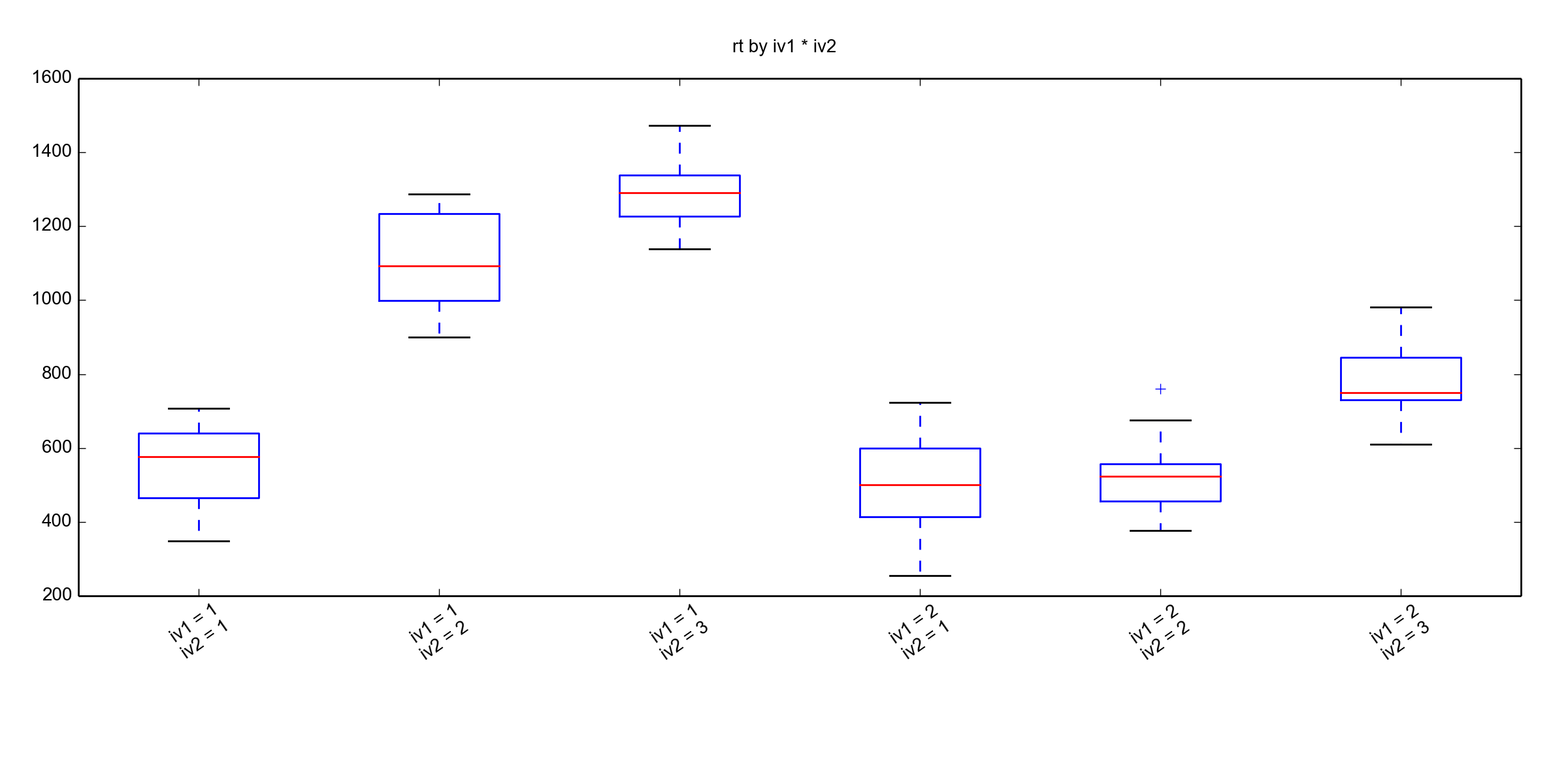
Two-way ANOVA for within-subjects design in Python
To run the Two-Way ANOVA is simple; the first argument is the dependent variable, the second the subject identifier, and then the within-subject factors. In two previous posts I showed how to carry out one-way and two-way ANOVA for independent measures. One could, of course, combine these techniques, to do a split-plot/mixed ANOVA by adding an argument ‘bfactors’ for the between-subject factor(s).
aov = df.anova('rt', sub='Sub_id', wfactors=['iv1', 'iv2'])
print(aov)Code language: Python (python)The output one gets from this is an ANOVA table. In this table all metrics needed plus some more can be found; F-statistic, p-value, mean square errors, confidence intervals, effect size (i.e., eta-squared) for all factors and the interaction. Also, some corrected degrees of freedom and mean square error can be found (e.g., Grenhouse-Geisser corrected). The output is in the end of the post. It is a bit hard to read. If you know any other way to do a repeated-measures ANOVA using Python please let me know. Also, if you happen to know that you can create nicer plots with Pyvttbl I would also like to know how! Please leave a comment.
Update (2017-07-03): If your installed version of Numpy is greater than 1.11.x, you will run into a Float and NoneType error. One quick solution for this is to downgrade Numpy to 1.11.x. I created a post, Step-by-step guide for solving the Pyvttbl Float and NoneType error, in which I show how to install Numpy 1.11.x in an virtual environment. This way, you can run your ANOVAs, without having to uninstall Numpy.
Output ANOVA table
rt ~ iv1 * iv2
TESTS OF WITHIN SUBJECTS EFFECTS
Measure: rt
Source Type III eps df MS F Sig. et2_G Obs. SE 95% CI lambda Obs.
SS Power
=======================================================================================================================================================
iv1 Sphericity Assumed 4419957.211 - 1 4419957.211 324.248 2.128e-13 3.295 60 16.096 31.548 1023.941 1
Greenhouse-Geisser 4419957.211 1 1 4419957.211 324.248 2.128e-13 3.295 60 16.096 31.548 1023.941 1
Huynh-Feldt 4419957.211 1 1 4419957.211 324.248 2.128e-13 3.295 60 16.096 31.548 1023.941 1
Box 4419957.211 1 1 4419957.211 324.248 2.128e-13 3.295 60 16.096 31.548 1023.941 1
-------------------------------------------------------------------------------------------------------------------------------------------------------
Error(iv1) Sphericity Assumed 258996.722 - 19 13631.406
Greenhouse-Geisser 258996.722 1 19 13631.406
Huynh-Feldt 258996.722 1 19 13631.406
Box 258996.722 1 19 13631.406
-------------------------------------------------------------------------------------------------------------------------------------------------------
iv2 Sphericity Assumed 5257766.564 - 2 2628883.282 206.008 4.023e-21 3.920 40 18.448 36.158 433.701 1
Greenhouse-Geisser 5257766.564 0.550 1.101 4777252.692 206.008 1.320e-12 3.920 40 18.448 36.158 433.701 1
Huynh-Feldt 5257766.564 0.550 1.101 4777252.692 206.008 1.320e-12 3.920 40 18.448 36.158 433.701 1
Box 5257766.564 0.500 1 5257766.564 206.008 1.192e-11 3.920 40 18.448 36.158 433.701 1
-------------------------------------------------------------------------------------------------------------------------------------------------------
Error(iv2) Sphericity Assumed 484921.251 - 38 12761.086
Greenhouse-Geisser 484921.251 0.550 20.911 23189.668
Huynh-Feldt 484921.251 0.550 20.911 23189.668
Box 484921.251 0.500 19 25522.171
-------------------------------------------------------------------------------------------------------------------------------------------------------
iv1 * Sphericity Assumed 1622027.598 - 2 811013.799 83.220 1.304e-14 1.209 20 22.799 44.687 87.600 1.000
iv2 Greenhouse-Geisser 1622027.598 0.545 1.091 1486817.582 83.220 6.085e-09 1.209 20 22.799 44.687 87.600 1.000
Huynh-Feldt 1622027.598 0.545 1.091 1486817.582 83.220 6.085e-09 1.209 20 22.799 44.687 87.600 1.000
Box 1622027.598 0.500 1 1622027.598 83.220 2.262e-08 1.209 20 22.799 44.687 87.600 1.000
-------------------------------------------------------------------------------------------------------------------------------------------------------
Error(iv1 * Sphericity Assumed 370327.311 - 38 9745.456
iv2) Greenhouse-Geisser 370327.311 0.545 20.728 17866.175
Huynh-Feldt 370327.311 0.545 20.728 17866.175
Box 370327.311 0.500 19 19490.911
TABLES OF ESTIMATED MARGINAL MEANS
Estimated Marginal Means for iv1
iv1 Mean Std. Error 95% Lower Bound 95% Upper Bound
==============================================================
1 983.755 43.162 899.157 1068.354
2 599.917 21.432 557.909 641.925
Estimated Marginal Means for iv2
iv2 Mean Std. Error 95% Lower Bound 95% Upper Bound
===============================================================
1 525.025 19.324 487.150 562.899
2 814.197 49.416 717.342 911.053
3 1036.286 43.789 950.459 1122.114
Estimated Marginal Means for iv1 * iv2
iv1 iv2 Mean Std. Error 95% Lower Bound 95% Upper Bound
=====================================================================
1 1 553.522 24.212 506.066 600.978
1 2 1103.488 28.411 1047.804 1159.173
1 3 1294.256 19.773 1255.501 1333.011
2 1 496.528 29.346 439.009 554.047
2 2 524.906 20.207 485.301 564.512
2 3 778.317 21.815 735.560 821.073
Alternative Data Analysis Techniques
In this section, you will find some blog posts that are covering other data analysis tecniques:
- How to Perform a Two-Sample T-test with Python: 3 Different Methods
- Probabilistic Programming in Python
- How to Perform Mann-Whitney U Test in Python with Scipy and Pingouin

Hi there. Thanks for your excellent blog. I’m trying to run a two-way repeated mesures ANOVA using pyvttbl as you explain. I use python 2.7 and installed pyvttbl via pip. I was able to import pyvttbl and create the dataframe just fine. However, when I run the test, I get this error: TypeError: unsupported operand type(s) for +: ‘float’ and ‘NoneType’. Can you help? Thanks in advance!
Hey Veronica,
Have you solved the problem? When I wrote this blog, this did not happen. However, I tried to run the script again and get the same problem. I am not sure what is going on here but I will try to find out given that you did not solve it.
Please let me know if and how you solved the problem.
Erik
Hi,
I’ve had the same error but by googling it, I found a similar issue with the library py-faster-rcnn (https://github.com/rbgirshick/py-faster-rcnn/issues/481#issuecomment-278709605). You have to uninstall the current version of numpy and install numpy v1.11.0. For me, it works !
Damien
Thanks for leaving your comment here, Damien!
I will update the posts later and reference to your solution.
Erik
Hi Erik,
I met the same problem when I ran my analysis. In my study, the design is a 2x3x3 repeated measure ANOVA. And my code is straightforward, import pyvttbl as pt
df = pt.DataFrame()
df.read_tbl(‘Z_score_filtered.csv’)
aov = df.anova(‘Z_score’, sub=’ID’, wfactors=[‘Task_types’, ‘conditions’, ‘Question’])
print(aov)
But it returned the error “unsupported operand type(s) for +: ‘float’ and ‘NoneType'”. I have checked my data file and found Z_score was stored as numpy.float64. Is it the reason I have this error message? Should I change my data from numpy.float64 to long or other data type?
Thanks for your help!
Hey Shengjie,
Right now I don’t have a solution for this problem other than the one Damien gave here in the comments. It seems like you have to have Python 1.11.0 (maybe other versions work to but it worked for Damien). Hope it helps. I will update my post(s) with this solution. I don’t think Pyvttbl have been updated for 4 years, or so. Maybe someone should build a new package/update Pyvttbl. 🙂