Three ways to do a two-way ANOVA with Python

In an earlier post, I showed four different techniques that enable a one-way analysis of variance (ANOVA) using Python. Now, in this Python data analysis tutorial, we are going to learn how to do two-way ANOVA for independent measures using Python.

First, we are going to learn how to calculate the ANOVA table “by hand”. Second, we are going to use Statsmodels and, third, we carry out the ANOVA in Python using pyvttbl. Finally, as a bonus, we will also use Pingouin Stats, a newer Python package.

• Save

An important advantage of the two-way ANOVA is that it is more efficient compared to the one-way. There are two assignable sources of variation – supp and dose in our example – and this helps to reduce error variation thereby making this design more efficient.

Two-way ANOVA (factorial) can be used to, for instance, compare the means of populations that are different in two ways. It can also be used to analyze the mean responses in an experiment with two factors. Unlike One-Way ANOVA, it enables us to test the effect of two factors at the same time.

One can also test for independence of the factors provided there are more than one observation in each cell. The only restriction is that the number of observations in each cell has to be equal (there is no such restriction in the case of one-way ANOVA).

We discussed linear models earlier – and ANOVA is indeed a kind of linear model – the difference being that ANOVA is where you have discrete factors whose effect on a continuous (variable) result you want to understand. Make sure to check the recent posts about how to perform two-sample t-test in Python and Mann-Whitney U-test in Python.

Table of Contents

• Python 2-way ANOVA
  • Calculation of Sum of Squares
    • Degrees of Freedom
    • Sum of Squares
      • Sum of Squares A – supp
      • Sum of Squares B – dose
      • Sum of Squares Total
      • Sum of Squares Within (error/residual)
      • Sum of Squares interaction
    • Mean Squares
      • Mean Square A
      • Mean Square B
      • Mean Square AxB
      • Mean Square Within/Error/Residual
    • F-ratio
    • Obtaining p-values
    • Output ANOVA table
  • Two-way ANOVA using Statsmodels
    • Output ANOVA table
  • Two-way ANOVA in Python using pyvttbl
  • Measure: len
• Two-Way ANOVA using Pingouin (Bonus)

Python 2-way ANOVA

First of all, we need to import all the tools neede to carry out the ANOVA:

import pandas as pdimport statsmodels.api as sm
from statsmodels.formula.api import ols
from statsmodels.stats.anova import anova_lm
from statsmodels.graphics.factorplots import interaction_plot
import matplotlib.pyplot as plt
from scipy import statsCode language: Python (python)

In the code above, we import all the needed Python libraries and methods for doing the two first methods using Python (calculation with Python and using Statsmodels). In the last, and third, a method for doing python ANOVA we are going to use Pyvttbl. As in the previous post on one-way ANOVA using Python, we will use a set of data that is available in R but can be downloaded here: TootGrowth Data. Pandas is used to create a dataframe that is easy to manipulate.

datafile = "ToothGrowth.csv"
data = pd.read_csv(datafile)Code language: Python (python)

It can be good to explore data before continuing with the inferential statistics. statsmodels has methods for visualizing factorial data. We are going to use the method interaction_plot.

fig = interaction_plot(data.dose, data.supp, data.len,
             colors=['red','blue'], markers=['D','^'], ms=10)Code language: Python (python)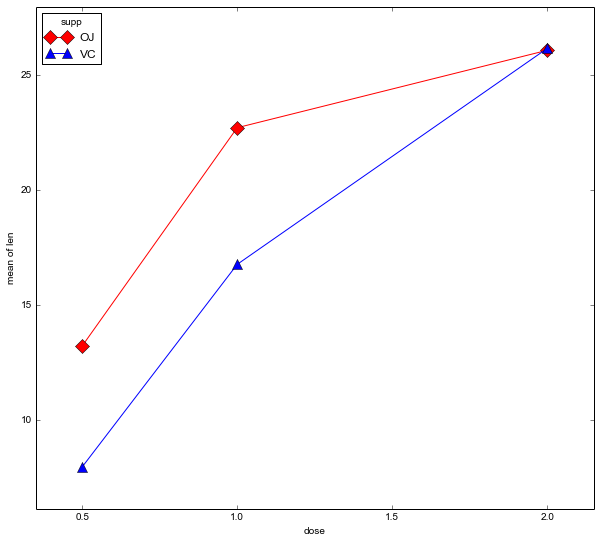

• Save

Calculation of Sum of Squares

The calculations of the sum of squares (the variance in the data) are quite simple using Python. First, we start with getting the sample size (N) and the degree of freedoms needed. We will use them later to calculate the mean square. After we have the degree of freedom we continue with the calculation of the sum of squares.

Degrees of Freedom

N = len(data.len)
df_a = len(data.supp.unique()) - 1
df_b = len(data.dose.unique()) - 1
df_axb = df_a*df_b 
df_w = N - (len(data.supp.unique())*len(data.dose.unique()))Code language: Python (python)

Sum of Squares

• Save

For the calculation of the sum of squares A, B and Total we will need to have the grand mean. Using Pandas DataFrame method mean on the dependent variable only will give us the grand mean:

grand_mean = data['len'].mean()Code language: Python (python)

The grand mean is simply the mean of all scores of len.

Sum of Squares A – supp

We start with calculation of Sum of Squares for the factor A (supp).

ssq_a = sum([(data[data.supp ==l].len.mean()-grand_mean)**2 for l in data.supp])Code language: Python (python)

Sum of Squares B – dose

Calculation of the second Sum of Square, B (dose), is pretty much the same but over the levels of that factor.

ssq_b = sum([(data[data.dose ==l].len.mean()-grand_mean)**2 for l in data.dose])<Code language: Python (python)

Sum of Squares Total

ssq_t = sum((data.len - grand_mean)**2)Code language: Python (python)

Sum of Squares Within (error/residual)

Next, we need to calculate the Sum of Squares Within which is sometimes referred to as error or residual.

vc = data[data.supp == 'VC']
oj = data[data.supp == 'OJ']
vc_dose_means = [vc[vc.dose == d].len.mean() for d in vc.dose]
oj_dose_means = [oj[oj.dose == d].len.mean() for d in oj.dose]
ssq_w = sum((oj.len - oj_dose_means)**2) +sum((vc.len - vc_dose_means)**2Code language: Python (python)

Sum of Squares interaction

Since we have a two-way design we need to calculate the Sum of Squares for the interaction of A and B.

ssq_axb = ssq_t-ssq_a-ssq_b-ssq_wCode language: Python (python)

Mean Squares

We continue with the calculation of the mean square for each factor, the interaction of the factors, and within.

Mean Square A

ms_a = ssq_a/df_aCode language: Python (python)

Mean Square B

ms_b = ssq_b/df_bCode language: Python (python)

Mean Square AxB

ms_axb = ssq_axb/df_axbCode language: Python (python)

Mean Square Within/Error/Residual

ms_w = ssq_w/df_wCode language: Python (python)

F-ratio

The F-statistic is simply the mean square for each effect and the interaction divided by the mean square for within (error/residual).

f_a = ms_a/ms_w
f_b = ms_b/ms_w
f_axb = ms_axb/ms_wCode language: Python (python)

Obtaining p-values

We can use the scipy.stats method f.sf to check if our obtained F-ratios is above the critical value. Doing that we need to use our F-value for each effect and interaction as well as the degrees of freedom for them, and the degree of freedom within.

p_a = stats.f.sf(f_a, df_a, df_w)
p_b = stats.f.sf(f_b, df_b, df_w)
p_axb = stats.f.sf(f_axb, df_axb, df_w)Code language: Python (python)

The results are, right now, stored in a lot of variables. To obtain a more readable result we can create a DataFrame that will contain our ANOVA table.

results = {'sum_sq':[ssq_a, ssq_b, ssq_axb, ssq_w],
           'df':[df_a, df_b, df_axb, df_w],
           'F':[f_a, f_b, f_axb, 'NaN'],
            'PR(>F)':[p_a, p_b, p_axb, 'NaN']}
columns=['sum_sq', 'df', 'F', 'PR(>F)']
aov_table1 = pd.DataFrame(results, columns=columns,
                          index=['supp', 'dose', 
                          'supp:dose', 'Residual'])Code language: Python (python)

As a Psychologist, most of the journals we publish in requires to report effect sizes. Common software, such as SPSS has eta squared as output. However, eta squared is an overestimation of the effect. To get a less biased effect size measure we can use omega squared. The following two functions add eta squared and omega squared to the above DataFrame that contains the ANOVA table.

def eta_squared(aov):
    aov['eta_sq'] = 'NaN'
    aov['eta_sq'] = aov[:-1]['sum_sq']/sum(aov['sum_sq'])
    return aov
def omega_squared(aov):
    mse = aov['sum_sq'][-1]/aov['df'][-1]
    aov['omega_sq'] = 'NaN'
    aov['omega_sq'] = (aov[:-1]['sum_sq']-(aov[:-1]['df']*mse))/(sum(aov['sum_sq'])+mse)
    return aov
eta_squared(aov_table1)
omega_squared(aov_table1)
print(aov_table1)Code language: Python (python)

Output ANOVA table

• Save

• Jupyter Notebook containing the code above

Two-way ANOVA using Statsmodels

There is, of course, a much easier way to do Two-way ANOVA with Python. We can use Statsmodels which have a similar model notation as many R-packages (e.g., lm). We start with the formulation of the model:

formula = 'len ~ C(supp) + C(dose) + C(supp):C(dose)'
model = ols(formula, data).fit()
aov_table = anova_lm(model, typ=2)Code language: Python (python)

Statsmodels does not calculate effect sizes for us. My functions above can, again, be used and will add omega and eta squared effect sizes to the ANOVA table. Actually, I created these two functions to enable calculation of omega and eta squared effect sizes on the output of Statsmodels anova_lm method. Note, statsmodels can be installed with e.g. pip or conda.

eta_squared(aov_table)
omega_squared(aov_table)
print(aov_table.round(4))Code language: Python (python)

Output ANOVA table

• Save

What is neat with using statsmodels is that we can also do some diagnostics. It is, for instance, very easy to take our model fit (the linear model fitted with the OLS method) and get a Quantile-Quantile (QQplot):

res = model.resid 
fig = sm.qqplot(res, 's')
plt.show()Code language: Python (python)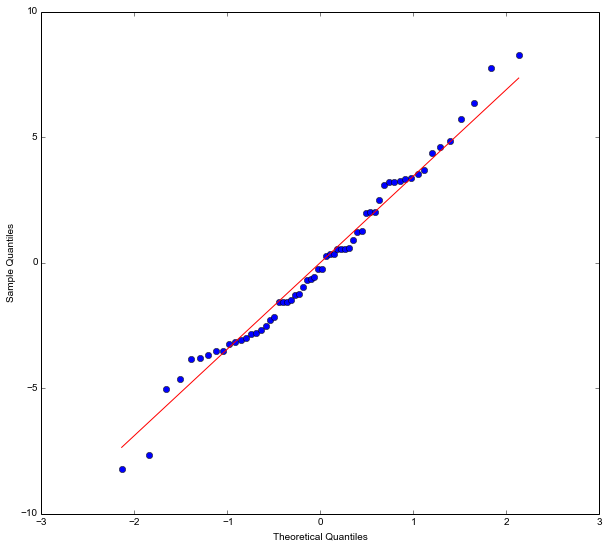

• Save

• Statsmodels 2-Way ANOVA Notebook

Two-way ANOVA in Python using pyvttbl

The third way to do Python ANOVA is by using the library pyvttbl. Pyvttbl has its own method (also called DataFrame) to create data frames.

from pyvttbl import DataFrame
df = DataFrame()
df.read_tbl(datafile)
df['id'] = xrange(len(df['len']))
print(df.anova('len', sub='id', bfactors=['supp', 'dose']))Code language: Python (python)

The ANOVA tables of Pyvttbl contains a lot of more information compared to that of statsmodels. Actually, Pyvttbl output contains an effect size measure; the generalized omega squared.

Measure: len

Source	Type III Sum of Squares	df	MS	F	Sig.	η2G	Obs.	SE of x̄	±95% CI	λ	Obs. Power
supp	205.350	1.000	205.350	15.572	0.000	0.224	30.000	0.678	1.329	8.651	0.823
dose	2426.434	2.000	1213.217	92.000	0.000	0.773	20.000	0.831	1.628	68.148	1.000
supp * dose	108.319	2.000	54.159	4.107	0.022	0.132	10.000	1.175	2.302	1.521	0.173
Error	712.106	54.000	13.187
Total	3452.209	59.000

Two-Way ANOVA using Pingouin (Bonus)

Here’s a bonus method to carry out ANOVA using Python; using the Python package Pingouin. Although pyvttbl is quite good, it’s not maintained any more. Here, Pingouin offers a very easy way to for ANOVA in Python.

import pandas as pd
import pingouin as pg
data = 'https://vincentarelbundock.github.io/Rdatasets/csv/datasets/ToothGrowth.csv'
df = pd.read_csv(data, index_col=0)
df.head()Code language: Python (python)

• Save

aov = pg.anova(dv='len', between=['supp', 'dose'], data=df,
             detailed=True)

print(aov)Code language: Python (python)

• Save

• Jupyter Notebook with the Pingouin ANOVA code example